티스토리 뷰
'기하'라는 말은 길이, 넓이가 수치적으로 얼마인가 를 뜻하는 말로서 시작되었습니다. 라틴어인 'Geometria'는 고대 그리스어에서 온 말이며, 이는 '땅'이라는 의미이고 측정하다 라는 뜻의 그리스어가 합하여져서 만들어진 단어입니다.
고전의 기하학은 어쩌면 당연한것들에 대한 연구로부터 시작되었습니다.
고전에 기하학에 대해 연구했던 잔해인 점토판을 보면, 이렇게 나타나 있습니다.
1. 임의의 서로 다른 두 점 P, Q에 대해 두 점을 지나는 직선은 유일하다.
2. 임의의 두 선분 AB, CD에 대해 B가 A와 E사이에 위치하고 선분 BE의 길이가 선분 CD의 길이와 같게 되는 점 E는 유일하다.
이게 무슨말이냐 싶으시겠지만 쉽게 말하자면, 두 개의 선분이 만난다면, 만나는 점은 단 하나이다 라는 뜻 입니다.
3. 점 O를 정점으로 하고 반지름이 OP인 원을 그릴 수 있다.
4. 모든 직각은 합동이다.
5. 하나의 직선위에 있지 않은 점 P를 지나는 평행선은 유일하다.
위의 내용이 기하학의 처음 연구이고 개발된 내용입니다. 위의 5가지 정리를 시작으로 기하학이 하나 둘 발전하게 되는데, 그 중 가장 쉽고 많이 아는 정리가 '피타고라스의 정리'입니다.
그럼 피타고라스의 정리에 대해 소개하지 않고 지나갈 순 없겠죠? 쉽지만, 꼭 언급하고 지나가야하는 피타고라스의 정리에 대해 이야기 해보겠습니다.
<피타고라스의 정리>
피타고라스의 정리는 유클리드 기하학에서 널리 알려진 기본 정리입니다. 직각삼각형의 세 변 a, b, c에서 c를 빗변이라고 할 때, a^2+b^2=c^2 가 된다는 정리입니다.
피타고라스의 정리는 수 많은 정리가 있지만, 그 중 하나는 중학생 정도의 수학능력이면 충분히 증명 할 수 있는 부분입니다.
피타고라스의 정리는 아래의 사진과 같이 증명합니다.
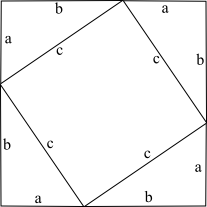
한 변의 길이를(a+b)이라고 하면 큰 정 사각형의 넓이는 (a+b)^2이 됩니다.
이번에는 각 부분의 넓이를 구해보면, 작은 정사각형의 넓이는 c^2, 네 개의 직각삼각형의 넓이는 ab/2*4가 됩니다.
따라서 전체의 넓이는 c^2+4*ab/2=c^2+2ab가 됩니다. 그러므로 이를 정리하면, (정리과정은 생략하겠습니다.)
a^2+b^2=c^2가 성립함을 알 수 있습니다.
이렇게 피타고라스의 정리는 간단한 도형만으로도 쉽게 증명이 가능합니다.
피타고라의의 정리는 너무도 잘 알려져 있으니, 이번에는 여러분들이 조금은 생소할 수 있도록 새로운 이야기를 해보도록 해보겠습니다.
원뿔곡선에 대한 이야기인데, 원뿔곡선은 고대그리스 시대에서부터 계속 되어왔던 연구입니다. 원뿔곡선은 하나의 평면으로 원뿔을 잘랐을 때 생기는 곡선인 원, 타원, 포물선, 쌍곡선을 말합니다. 각 곡선에 대한 기하학의 정의는 아래와 같습니다.
원: 평면위의 하나의 정점에서 거리가 일정한 점들의 집합
타원: 평면 위의 두 정점에서 거리의 합이 일정한 점들의 집합
포물선: 평면 위의 하나의 정점과 이를 지나지 않는 하나의 직선에서 같은 거리에 있는 점들의 집합
쌍곡선: 평면 위의 두 정점에서 거리의 차가 일정한 점들의 집합
으로 기하학에서 정의되고 있습니다. 위의 원, 타원, 포물선, 쌍곡선은 식으로 나타내게 되면, 원의 방정식, 타원의 방정식, 포물선의 방정식, 쌍곡선의 방정식으로 표현되는데, 이 방정식들은 같은 방정식으로 표현되고 모양에 따라서 크기에 따라서 계수가 변할 뿐 기본적인 틀은 일치합니다.
일상생활속 가장 가깝다고 느끼실 '원'만 예를 들어도 원과 관련된 엄청나게 다양한 용어들이 있고, 그 용어들을 사용한 많은 정리들, 그리고 많은 증명들이 있습니다.
원은 상당히도 재미있는 도형입니다.
기원전 5세기 경 안티폰이라는 학자는 정다각형의 변수를 계속 늘려가면 결국 원이 될 것이라고 생각했습니다. 그러나 15세기 독일의 신학자 니콜라우스는 아무리 변을 늘려도 원은 딜 수 없다는 사상으로 반박했습니다.
여러분들은 어떻게 생각하시나요? 정다각형의 변수를 무한대로 늘린다면 그 도형은 원이 될 수 있을까요?
무한소수 0.9999999.....를 우리는 분수로 나타내었을 때 1로 칭하곤 하지 않습니까? 저도 확실한 답은 알지 못하지만, 아마 원과 정다각형의 넓이를 이용해 증명을 하지 않았을까 생각이 듭니다.
기회가 된다면 이 문제에 대해서도 이야기 해보고 넘어가도록 하겠습니다.
앞으로의 시간부터는 다른 분야의 수학에 대해 이야기 하기 전 기하학의 세부적인 부분부터 살펴보고자 해보겠습니다.
다음 시간에는 원에 대해 더 자세하게 이야기해보도록 하겠습니다.
원에 대한 이야기가 궁금하시다면 다음 포스팅에 꼭 오시길 바랍니다.
- Total
- Today
- Yesterday
- 수학의역사 #산술 #대수학 #기하학 #해석학 #이산수학 #고드프리하디 #수학자명언
- 수학 #수학이란 #수학의역사 #자연과학 #수학과
- 원 #타원 #쌍곡선 #포물선 #원뿔 #기하학 #피타고라스의정리 #피타고라스의정리증명 #피타고라스
- 군 환 체 #대수학 #현대대수학 #대수학의역사 #기하학 #갈루아
- 페르마의 마지막 정리 #수의체계 #부분집합 #산술 #자연수 #정수 #실수 #유리수
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
